Lunisolar Calendar - Calculate lunar calendar like Vietnamese (or Chinese) based on your own timezone

1. How to use Lunisolar Calendar app

With Lunisolar Calendar app, users can select a day or a month in the common calendar to see the equivalent dates in Vietnamese Lunar Calendar. The required inputs are:

• Day (if you select a day): It has to be a positive integer not greater than the maximum day of a particular month (28, 29, 30, or 31)
• Month: It is from January to December
• Year: It has to be a positive integer. If you are willing to look up a Before Common Era year, do select the BCE option below
• BCE or CE: It is the option for Before Common Era or Common Era
• New Moon soure: It is the data source for New Moon moments. This option will be explained more detail at section 3.3
• UTC offset: It is your timezone's time offset. For example, Vietnamese use UTC+7
• Language: Your calendar will use the chosen language. The default language is English

After pressing the "Search" buttons, if there is anything not right, this tool will have a notification. And if there hasn't been the Lunisolar Calendar data for the chosen dates, this tool will display Lunisolar Calendar date as 0 or TBD.

In the table of month calendar, you can click a particular cell of days to see the detailed day calendar.

2. How Vietnamese calculate the Lunisolar Calendar

2.1. Overview of Vietnamese Lunisolar Calendar

The Traditional Vietnamese Lunisolar Calendar, or Lunar Calendar, is based on moon phases but not just that. It's not purely lunar calendar like the Islamic one. It's combined with the solar year (based on the Sun), or tropical year specifically. People usually call the Vietnamese calendar as lunar calendar, but it's actually in lunisolar category. Of course there are some other lunisolar calendars around the world, they differ each other in calculating rules and which type of the "solar part" they use.

Vietnamese Lunisolar Calendar is used to have an important role, since moon phases help people know clearly about water tides or make plan for activities at night. Meanwhile it's also in a rough agreement with the solar year, meaning roughly synchronized with seasons and weather cycles. Nowadays, Vietnamese Lunisolar Calendar is the fundamental of folk cultures, religions, or the identification of traditional festivals, events and memorial days... It's accompanied with Five Agents/Elements (Fire, Water, Wood, Metal, Earth), or Heavenly Sterms and Earthly Branches.

In general, Vietnamese Lunisolar/Lunar Calendar has intercalation rules to add intercalary/leap month everytime it drift too far away from the synchronization with the solar year. But before diving in the detailed rules, we have to be clear on some concepts and definitions in astrology.

2.2. Basic concepts and definitions in calendar calculating

In astronomy, the Ecliptic Coordinate System is a celestial coordinate system commonly used for representing the apparent positions, orbits, and pole orientations of Solar System objects. With the Earth-centered Ecliptic Coordinate System, we have the Celestial Sphere which is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the Celestial Sphere. Half of the sphere would resemble a hemispherical screen over the observing location, it's the observer's visible sky.

Certain reference lines and planes on Earth, when projected onto the Celestial Sphere, form the bases of the reference systems. These include the Earth's equator, axis, and orbit. At their intersections with the Celestial Sphere, these form the Celestial Equator, the north and south celestial poles, and the Ecliptic, respectively. The Ecliptic or ecliptic plane is the orbital plane of Earth around the Sun, or the orbit of Sun around the Earth in this artificial Earth-centered system. Based on the Ecliptic, Celestial Sphere also has Ecliptic Longitude and Ecliptic Latitude.

Because Earth's rotational axis is not perpendicular to its orbital plane, Earth's equatorial plane is not coplanar with the ecliptic plane, but is inclined to it by an angle of about 23.4°, which is known as the obliquity of the ecliptic. If the equator is projected outward to the Celestial Sphere, forming the Celestial Equator, it crosses the Ecliptic at two points known as the Equinoxes.

The coordinate origin, where both Ecliptic Longitude and Ecliptic Latitude equals 0, is the intersection of the Celestial Equator and the Ecliptic from which the Sun is northward. This point is called March Equinox (or vernal equinox, or spring equinox). The other intersection from which the Sun is southward is called September Equinox (or autumnal equinox, or fall equinox).

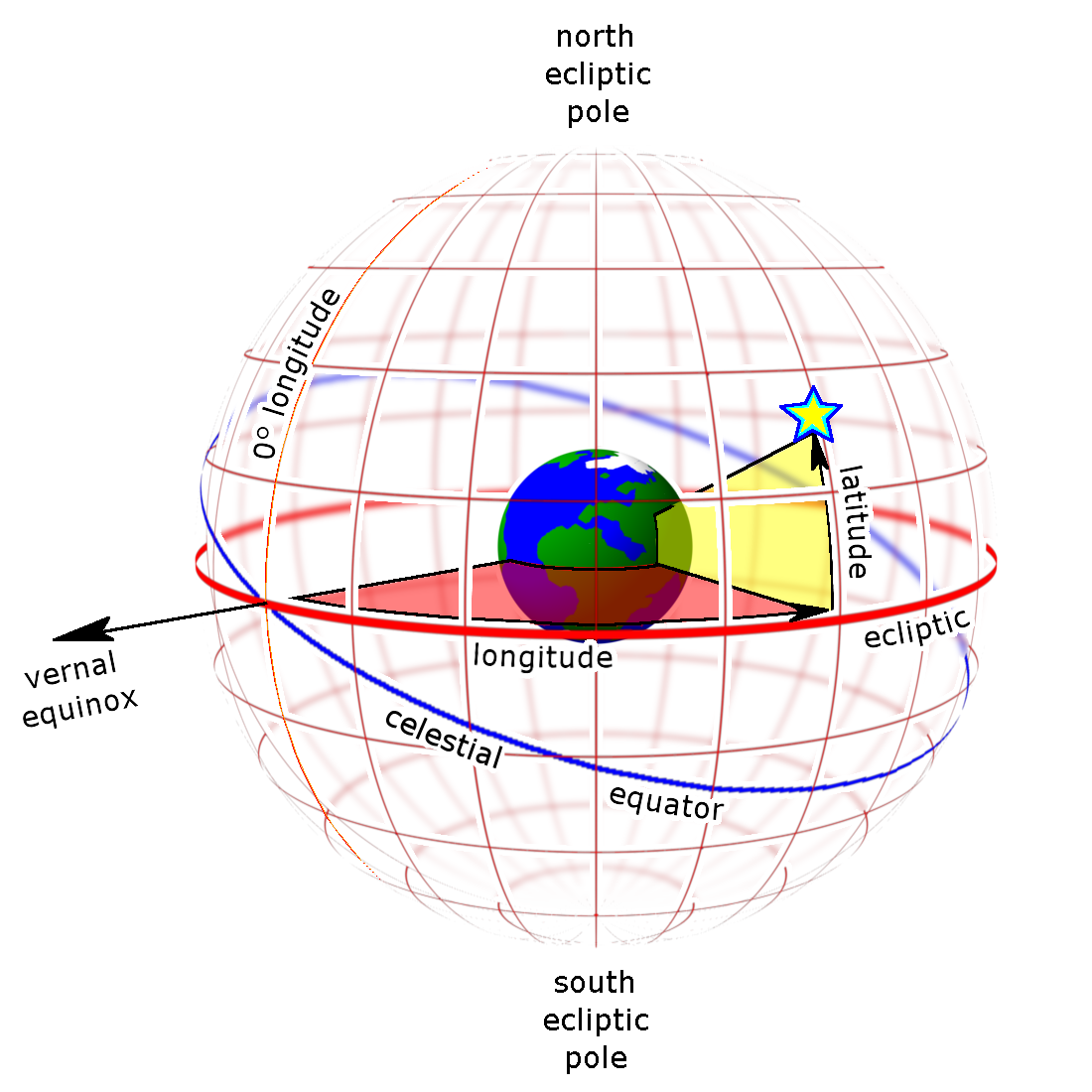
Along the Ecliptic, there are twenty-four periods call Solar Terms. The points are spaced 15° apart in Ecliptic Longitude. Among 24 Solar Terms, 12 of them are also called Major Solar Terms. The March Equinox is also the beginning of a Major Solar Term with Ecliptic Longitude 0°, called Xuân Phân (or Chunfen); the September Equinox is the beginning of another Major Solar Term with Ecliptic Longitude 180°, called Thu Phân (or Qiufen).

As other celestial objects, the Moon also has its own Ecliptic Longitude and Ecliptic Latitude. So when the Moon and Sun have the same Ecliptic Longitude, it's the first lunar phase, called the New Moon. At this phase, the lunar disk is not visible to the naked eye, except when it is silhouetted/shadowed against the Sun during a solar eclipse (when the Moon and Sun have the same Ecliptic Latitude too). When the Moon and Sun have the Ecliptic Longitude's difference of 180°, it's the Full Moon.

A Lunar Month (or synodic month, or lunation) is the time between two successive New Moons (or Full Moons). Currently, the average length of a Lunar Month is 29.53059 days^[1] (although this length can vary from 29.26 to 29.80 days). In a normal lunar year with 12 lunar months, the average length is 354,36708 days.

Meanwhile a solar year is the time that the Sun takes to return to the same position in the sky, for example it is the time from a March Equinox to the next March Equinox. The average length of this time is 365,24219^[1] days, 10,87511 days longer than a normal lunar year. After 3 years like that, the difference will expand to 32,62533 days, which is a little longer than a lunar month. So we fix it by add a 13th lunar month to the 3rd lunar year.

Another basic concept is The Julian Day Number (JDN), which is the number of days since the noon Universal Time on Monday, January 1st, 4713 BCE/BC, proleptic Julian calendar. "Proleptic" means the Julian calendar is extended backwards to dates preceding the year of 8 CE/AD when the quadrennial leap year is stabilized, not erratic anymore. You can read more about the Julian calendar at section 3.1.

2.3. The detailed calculating rules

The calculating rules of Vietnamese Lunisolar Calendar include these principles^[2][3] as follows:

• The first day of a Lunar Month is the day that includes New Moon. For example, there is a New Moon at 16:57 April 21st 2031 (UTC+0), equivalent to 23:57 the same day in Vietnam (UTC+7). So with Vietnamese, April 21st 2031 is the first day of a Lunar Month. If by some reasons, this New Moon is shifted some minutes to 0:00 April 22nd 2031 (UTC+7), then Vietnamese will consider April 22nd 2031 is the first day of a Lunar Month instead. A Lunar Month can have an integer number of days, so it will be 29 or 30 on a case-by-case basis.
• Similarly, the day that includes the beginning moment of a Solar Term will be considerd the beginning day of this Solar Term. It's true even if the beginning moment is 23:59:59.999. The Lunar Month of the beginning day of a Solar Term is considered "owning" this Solar Term.
• Đông Chí (or Dongzhi), the last Solar Term in a common year with Ecliptic Longitude 270° and the beginning marked by the December Solstice, must be scheduled in the Lunar Eleventh Month.
• Normally there are 12 lunar months between an Lunar Eleventh Month and the next Lunar Eleventh Month. But if there are 13 lunar months in this duration, it's when a lunar month will be considered the leap month. The leap month will be the first one in this duration that not own any Major Solar Term.
• Vietnamese Lunisolar Calendar is based on UTC+7 (GMT+7), it's actually slightly different with Chinese Lunisolar Calendar which based on UTC+8 (although all other rules are the same). According to the above example, there is a New Moon at 16:57 April 21st 2031 (UTC+0). With Vietnamese, April 21st 2031 is the first day of a Lunar Month because it's based on UTC+7. But with Chinese, the first day of a Lunar Month is April 22nd instead because based on UTC+8, the New Moon is at 0:57 this day.

With the difference in time offset between Vietnam and China, sometimes the Lunar New Year of the 2 countries are up to 1 month apart. However, with similar functions and data sources, these 2 calendars are still in synchronization. One country may have 29 days this lunar month and 30 days the next lunar month, another country may have 30 days this lunar month and 29 days the next lunar month, but generally the total days of 2 lunar month will be 59. One country may have 12 months in this lunar year and 13 months in the next lunar year, another country may have 13 months in this lunar year and 12 months in the next lunar year, but generally the total months of 2 lunar year will be 25.

If we apply the same calculating rules for other time offsets around the world, the ratio of mismatch with Vietnamese Lunar Calendar may become higher, but the self-healing synchronization will be still there. The calculation based on time offsets other than UTC+7 and UTC+8 is only hypothetical and mathematical, but this Lunisolar Callendar app is still ready to support it for researching purposes.

3. The foundations and solutions that HAHTech chooses to utilize

3.1. Which solar year will be used?

The Gregorian Calendar is the calendar used in most parts of the world now, including Vietnam. This calendar will be able to be used stably in the far future. However in the history of mankind, people did use the Julian Calendar for a long time. The difference between these 2 solar calendars is pretty tiny, but it's big enough to make effects.

With the Julian Calendar, there are 365 days in every year with an additional leap day every fourth year,without any exception. It means the Julian calendar was based on the estimate that the average solar year is exactly 365.25 days long, 0,00781 days longer than the more-precise cycle of a solar year mentioned at section 2.2 (365,24219 days). In a short term, the difference is almost nothing; but after about 1500 years of applying the Julian Calendar, an actual March Equinox became up to 12 days (11,715 days) earlier than itself in calendar.

So from October 1582, people started using the Gregorian Calendar. The rule for leap years in the Gregorian Calendar is that every year divisible by four is a leap year, except for years that are divisible by 100, except in turn for years also divisible by 400. For example, 1800, 1900, or 2100... is not leap years, but 2000 is. It makes the average solar year 365.2425 days long, just 0,00031 days longer than the precise cycle (365,24219 days). With this rule, it takes 3226 years for an actual March Equinox became 1 days earlier than itself in calendar.

Back to October 1582, people had to do something to fix the differential days caused by the Julian Calendar. The reform was done by advancing the date by 10 days, so Thursday 4 October 1582 was followed by Friday 15 October 1582, there is no date in between. This imperfect fixation is accepted widely in many calendar systems including Lunisolar Calendar app.

So from 15 October 1582 onward, we use the Gregorian Calendar; and from 4 October 1582 backward, we use the Julian Calendar or more specifically, the proleptic Julian calendar as mentioned at section 2.2. For a better understanding, the noon Universal Time on January 1st 4713 BCE has the JDN equaling 0; January 1st 1 CE has the JDN equaling 1721424; and January 1st 2025 CE has the JDN equaling 2460706.

The Gregorian Calendar inherited the JDN counting, so 4 October 1582 has the JDN of 2299160, and 15 October 1582 has the JDN of 2299161...

The lunisolar calendar calculated by this app is also "proleptic", because the rules did actually evolve in its entire history before solidating nowadays^[4].

3.2. How to know when Solar Terms are

HAHTech uses a function calculating the Sun's Ecliptic Longitude for each JDN value, that will help finding Solar Terms. This function is introduced by a researcher named Hồ Ngọc Đức, and it's more advance than the common function in Wiki^[5] when including the effect of nutation và aberration.

The function above is written in PHP, it will bring us results from 0 to 2 Pi (radian).

3.3. How to know when New Moons are

By a common function:

To know when New Moons happen, we have a common function shared on Wiki^[5]

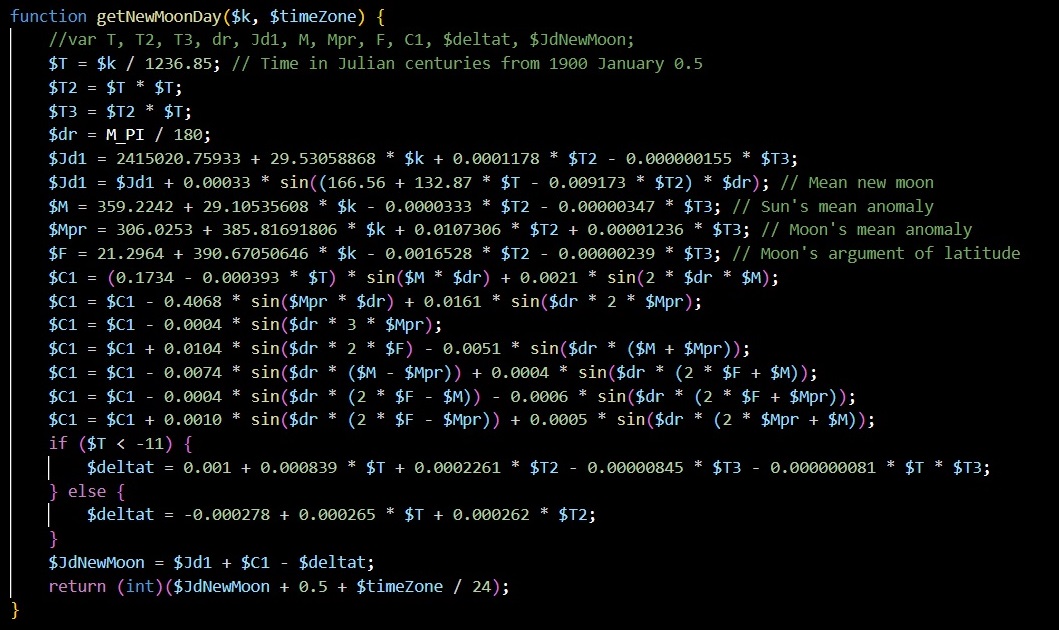
The function above is written in PHP, it calculates the JDN of New Moons with the zero point at the New Moon in January 1st 1900 (New Moon 0). The New Moons number 1, 2, 3... are from this zero point onward, while the New Moons number -1, -2, -3... are from this zero point backward.

This calculating is pretty precise, it can be utilized well by calendar apps in the near future. But for the far future or history researching, we may need some other calculating models or data sources.

By the data of AstroPixels:

There is a source of New Moons data that HAHTech applied in Lunisolar Calendar app, it's AstroPixels.com^[6]. This website has data of New Moons from 2000 BCE to 4000 CE.

The differences which are usually just a few minutes between 2 methods of identifying New Moons almost make no effect with Vietnamese lunisolar calendar in the near future (or past), until 2072. According to the common function, year of 2072 will have a New Moon at 0:01 December 10th (UTC+7); however according to the data of AstroPixels, this New Moon is at 23:59 December 9th. It's just 2 minutes but will make the lunisolar calendars calculated based on 2 methods being mismatch.

Similarly, in 2085, a New Moon is at 23:59 October 18th according to the common function, but also at 0:00 October 19th according to AstroPixels.

We can notice that the data of AstroPixels match with results answered by the astronomical online tool of US Navy, one of the most trusted sources in the world. This is why HAHTech also supports calculating lunisolar calendar based on AstroPixels.

3.4. The detailed calculating solutions in Lunisolar Calendar

By a common function:

If utilizing the function at section 3.2 combined with the common function at section 3.3, we will need to find some parameters as follows to calculate the lunisolar calendar with a chosen solar year:

• kLastYear11: the counting number of the New Moon of the Lunar Eleventh Month in the year right before the chosen solar year.
• kThisYear11: the counting number of the New Moon of the Lunar Eleventh Month in the chosen solar year.
• kNextYear11: the counting number of the New Moon of the Lunar Eleventh Month in the year right after the chosen solar year.
• kThisYear1: the counting number of the New Moon of the Lunar First Month in the chosen solar year.
• kNextYear1: the counting number of the New Moon of the Lunar First Month in the year right after the chosen solar year.
• kLeapMonth: the counting number of the New Moon of the Lunar Leap Month in the chosen solar year (it equals 0 if there is no leap month).

Among the parameters above, kThisYear1, kNextYear1, and kLeapMonth is targeted parameters which directly help indentifying when the lunisolar year starts, when it ends, the length of lunar months, and the length of of lunar leap month if there is a leap month.

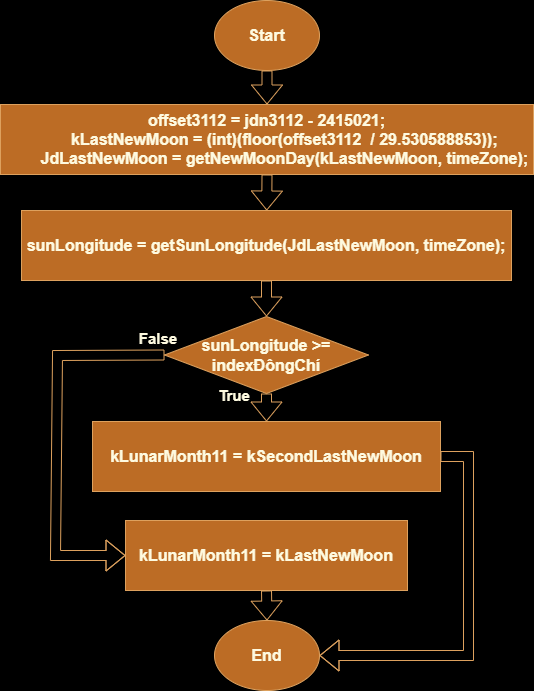
To find the New Moon of the Lunar Eleventh Month in any solar year, we will need:

• jdn3112: the JDN value of December 31st in the year in question.
• kLastNewMoon: the counting number of the last New Moon in the solar year in question.
• JdLastNewMoon: the JDN value of the last New Moon in the solar year in question.
• kSecondLastNewMoon: the counting number of the second-last New Moon in the solar year in question.
• sunLongitude: the index of the Solar Term coresponding to JdLastNewMoon. 24 indexes for 24 Solar Terms are from 0 to 23, and the index of Đông Chí is 18.
• kLunarMonth11 (the output): the counting number of the New Moon of the Lunar Eleventh Month in the solar year in question.

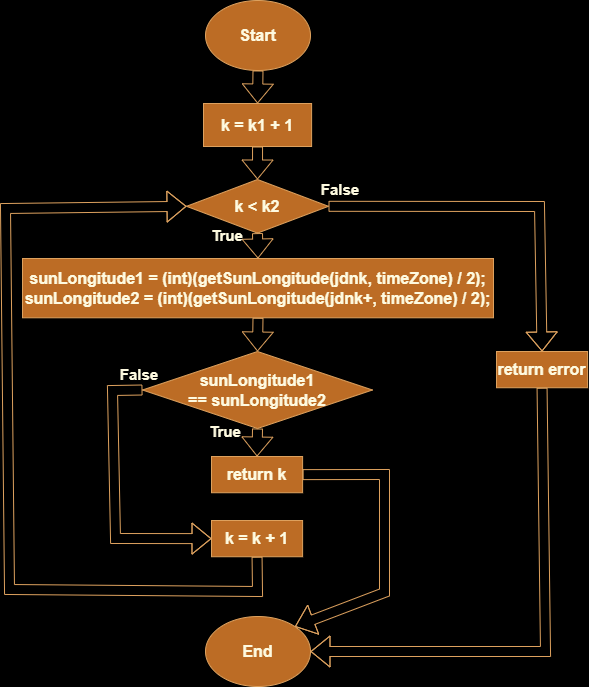
To find the New Moon of the Lunar Leap Month in any cycle between a Lunar Eleventh Month and the next Lunar Eleventh Month, we will need:

• k1 (the input): the counting number of the New Moon of the Lunar Eleventh Month in year 1 in question
• k2 (the input): the counting number of the New Moon of the Lunar Eleventh Month in year 2 in question
• jdnk: the JDN value of the New Moon number k
• jdnk+: the JDN value of the New Moon right after the New Moon number k
• sunLongitude1, sunLongitude2: the index of the Solar Term coresponding to jdnk and jdnk+
• k (the ouput): the variable k, checked in a range from k1+1 to k2-1.

By the data of AstroPixels:

If utilizing the function at section 3.2 combined with the data of AstroPixels, we will have arrays of New Moon dates for every relevant solar year. Each array will have a counting number of elements (count), and a range of index from 0 to count-1. From that, We will need to find some parameters as follows to calculate the lunisolar calendar with a chosen solar year:

• indexLastYear11: the index of the New Moon of the Lunar Eleventh Month in the year right before the chosen solar year.
• indexThisYear11: the index of the New Moon of the Lunar Eleventh Month in the chosen solar year.
• indexNextYear11: the index of the New Moon of the Lunar Eleventh Month in the year right after the chosen solar year.
• indexThisYear1: the index of the New Moon of the Lunar First Month in the chosen solar year.
• indexNextYear1: the index of the New Moon of the Lunar First Month in the year right after the chosen solar year.
• indexLeapMonth: the index of the New Moon of the Lunar Leap Month in the chosen solar year (it equals -1 if there is no leap month).

Among the parameters above, indexThisYear1, indexNextYear1, countThisYearNewMoon, and indexLeapMonth is targeted parameters which directly help indentifying when the lunisolar year starts, when it ends, the length of lunar months, and the length of of lunar leap month if there is a leap month.

To find the New Moon of the Lunar Eleventh Month in any solar year, we will need:

• indexLastNewMoon: the index of the last New Moon in the solar year in question.
• JdLastNewMoon: the JDN value of the last New Moon in the solar year in question.
• indexSecondLastNewMoon: the index of the second-last New Moon in the solar year in question.
• sunLongitude: the index of the Solar Term coresponding to JdLastNewMoon. 24 indexes for 24 Solar Terms are from 0 to 23, and the index of Đông Chí is 18.
• indexLunarMonth11 (the output): the index of the New Moon of the Lunar Eleventh Month in the solar year in question.

To find the New Moon of the Lunar Leap Month in any cycle between a Lunar Eleventh Month and the next Lunar Eleventh Month, we will need:

• index1st11 (the input): the index of the New Moon of the Lunar Eleventh Month in year 1 in question
• index2nd11 (the input): the index of the New Moon of the Lunar Eleventh Month in year 2 in question
• index1stMax: the index of the last New Moon in year 1 in question
• jdn1stMax: the JDN value of the last New Moon in year 1 in question
• jdn2nd0: the JDN value of the first New Moon in year 2 in question
• jdnindex: the JDN value of the New Moon with a particular index
• jdnindex+: the JDN value of the New Moon right after the New Moon with a particular index
• sunLongitude1, sunLongitude2: the index of the Solar Term coresponding to jdnindex and jdnindex+
• count1: the number of New Moons in year 1 in question (= index1stMax + 1)
• index (the output): the variable index, checked in a range from 0 to index2nd11-1.

3.5. What to do next

The orbits of the Earth and the Moon are both influenced by millions of celestial objects, causing countless fluctuations. In a short term, many of the minor variations can be ignored, but over long periods, they accumulate and have significant effects. Additionally, the duration of one Earth rotation - the basis of our definition of a "day" - is not constant. It can change due to major geological events and, to a lesser extent, even living creatures's activities.

For those reasons, HAHTech will always be ready to add and update the data sources for Lunisolar Calendar app. Instead of using the function at section 3.2, Lunisolar Calendar app can also process with a list of Major Solar Terms data in the years in question, we have solutions for it. The functions can also be more detail, or with new epochs.

The most important thing is, we have algorithms to calculate the lunisolar calendar based on valuable traditional rules with any data. So Lunisolar Calendar app can be used casually and daily, otherwise is also a tool for reasearching and AI training...

References

[1] P. Kenneth Seidelmann, ed. (1992). Explanatory Supplement to the Astronomical Almanac, p. 576. Publisher: University Science Books. ISBN: 978-0-935702-68-2.

[2] The article titled Cách tính lịch dương sang lịch âm, Giáo dục & Thời đại newspaper, November 15th 2024

[3] Webpage Thuật toán tính âm lịch, of researcher Hồ Ngọc Đức

[4] The circular 01-VLĐC August 19th 1967, posted on thuvienphapluat.vn

[5] The Wiki page called Mô đun:Âm lịch

[6] Moon Phases Table courtesy of Fred Espenak: Six Millennium Catalog of Phases of the Moon

Some other relevant Wiki pages